2022 计量2 课程内容 后面发现问题出在没有学过随机过程
我首先评论一下时间序列,AR Process 是与我之前学过的东西关系最紧密的内容(在计量2中),它是Inhomogeneous Linear Difference Equation 常数项换成了一个白噪声,而这个非齐次线性差分方程在计算递归算法复杂度的时候也经常遇到;而且他基本上就是微分方程的离散形式。
首先关于线性差分方程,一般的解法 是直接猜测形式是\(u_n=Aw^n\),也可以 证明线性差分方程的解的形式一定是\(u_n=A_1w_1^n+A_2w_2^n+\ldots\) 这种形式。 特征方程的所有解(假设无重根)的n次方都是一个特解, 根据给定的k个初值可以确定一个特解,而且对于任意一个初始解,带入特征方程得到的k个解中正好形成一个k行的线性方程组, 左侧系数是一个Vandermonde行列式,一定有解。
充分和必要条件 > 充分条件的证明:(宋翔羽写的) 考虑 \(|\alpha|>1\) 的多项式,证明前后两项的模长不相同 → 前后两项不相等 → \(|\alpha|>1\) 没有根 > 必要条件:(卿鸿杰写的) 构造多项式\(\Pi (1-x_i)\), 韦达定理可以凑出结果
1 Weakly Stationarity
The process \(\{X_t, t \in T\}\) is said to be weakly stationary (or covariance stationary or second-order stationary) if \(E(X_t^2 ) < \infty\) and both \(EX_t\) and \(Cov(X_t, X_{t+h})\), for any integer \(h\), do not depend on \(t\).
2 Differencial & Difference?
links-between-difference-and-differential-equations
3 AR(p) Weakly Stationarity
\[ \begin{aligned} y_t=\phi_0 +\phi_1y_{t-1}+&\ldots+\phi_p y_{t-p}+\epsilon_t\\ (1-\phi_1L-\phi_2L^2-\ldots-\phi_p L^p)y_t&=\phi_0+\epsilon_t\\ \end{aligned} \]
\[ [(1-L/x_1)(1-L/x_2)\ldots(1-L/x_p)]y_t=\phi_0+\epsilon_t\\ \]
\[ [1-(\phi_1+\phi_2L+\ldots+\phi_pL^{p-1})L]y_t=\phi_0+\epsilon_t\\ \]
where \(L\) is the lag-operator.
对于1,如果\((1-Lx_1), (1-Lx_2)\ldots\) 都可逆(也就是都能写成\((1+x_1L+x_1^2L^2+\ldots)(1+x_2L+x_2^2L^2+\ldots)\ldots(1+x_pL+x_p^2L^2+\ldots) \epsilon_t\) ), 就能轻松将一个AR(p)转化成一个MA(inf);对于2,如果\(1-(\phi_1-\phi_2L-\ldots)L\)可逆也可以转化成MA(inf)
对于MA(inf),期望\(E(y_t)=\mu\),方差\(Var(y_t)=\sigma^2 \sum_{j=0}^{\inf}\theta_j^2\), 需要让方差收敛.
对于1, 考虑\(\epsilon_{t-i}\)前面的系数, \(\epsilon_{t-i}\)需要在前面的p个括号中每个括号选择一项,我们尝试写出几项:
\[ \begin{aligned} i=1 \quad & \sum x_i\\ i=2 \quad & \sum x_i^2+\sum_{i<j} x_i x_j\\ i=3 \quad & \sum x_i^3+\sum_{i<j} x_i^2 x_j+\sum_{i<j} x_i x_j^2+\sum_{i<j<k} x_i x_j x_k\\ \ldots \end{aligned} \]
Time Series Analysis James D. Hamilton page35,用另外一种方法推出上面的系数
Time Series Analysis James D. Hamilton page35 [2.4.13] 这种系数的写法可以较为容易的证明出系数是绝对收敛的,而用上面列出的形式较为困难(我不会)
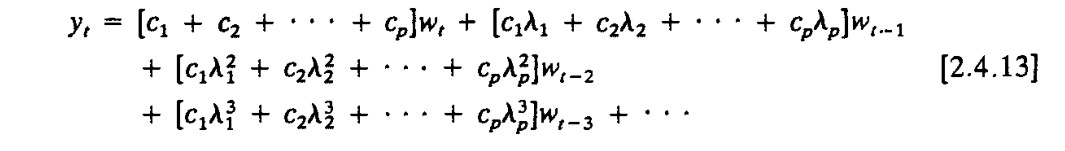
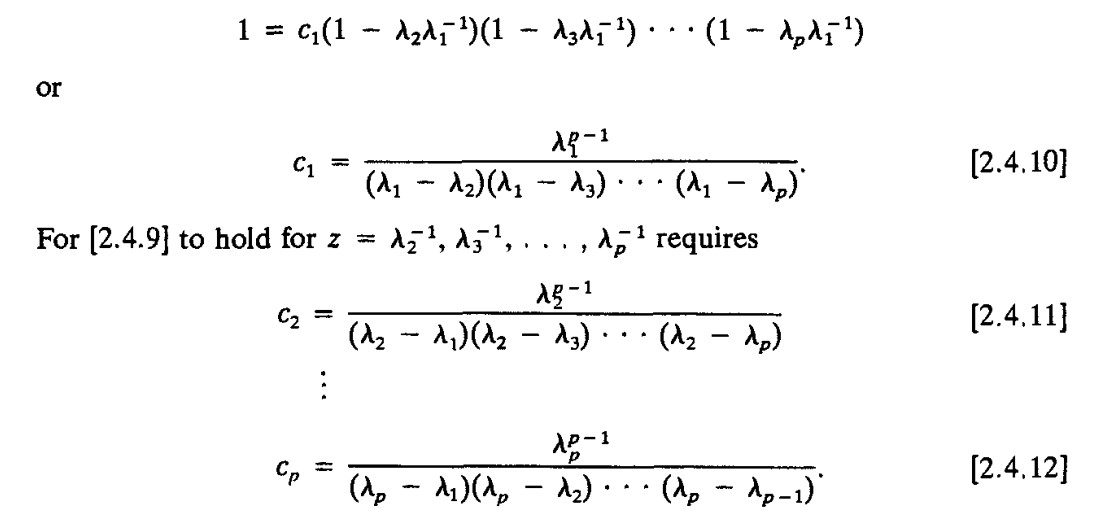
这里 c 的计算本身也非常有趣,见书35页左右
再考虑2,首先记得充分和必要条件当中的必要条件是系数和小于1,而2的这个形式 \(1-(\phi_1-\phi_2L-\ldots-\phi_pL^{p-1})L\)如果想要可逆,自然有\(\sum_{i=1}^p \phi_i<1\)
那么可以写成:
\[ y_t=\phi_0/(1-\phi_1-\ldots-\phi_p)+\\ [1+(\phi_1L+\ldots+\phi_pL^p)+(\phi_1L+\ldots+\phi_pL^p)^2+\ldots]\epsilon_t \]
然后尝试写出\(\epsilon_{t-i}\)的系数
\[ \begin{aligned} i=0 \quad & 1\\ i=1 \quad & \phi_1\\ i=2 \quad & \phi_1^2+\phi_2\\ \ldots \end{aligned} \]
和1的系数比较,\(i=1\)时\(\sum x_i=\phi_1\)(韦达定理,\(x_i\)是特征方程根的倒数); \(i=2\)时,\(\sum x_i^2+\sum_{i<j} x_i x_j=\phi_1^2+\phi_2\) (这里\(\sum x_i^2 = \phi_1^2+2\phi_2,\quad \sum_{i<j} x_i x_j=-\phi_2\))
可以发现这两种方法实际上是等价的
4 Questions?
- 能否构造出一个随机变量的期望与时间有关而任意两个随机变量的协方差与时间无关(或者反之)的时间序列