寒假听到一个问题,家族中有多少对父子多少对爷爷和孙子,问家族中人数最少有几人。
把这个问题变成,考虑一个DAG,给出DAG中长度(边的数量)为 \(l_i\) 的路径的数量 \(a_i\) ,求出顶点数量最少的满足条件的DAG
1 一个更简单的版本?
如果不是一般的 DAG ,而是一个 arborescence ?
嗯… \(|V|=|E|+t\), \(t\)是树的个数.
- 长度越长的路径显然数量要少于长度短的路径数量
- 如果只有一个约束(长度为\(l\)的路径数量是\(a\)), 可以贪心解决
1.1 2/6 点数的upperbound?
arborescence 情况下, 点数的上界是\(\sum a_i(l_i+1)\).
(\(a_i(l_i+1)\)的排序与\(l_i\)的排序应该是没什么关系的)
也许能够证明最优解中点数的上界是 \(\max \{a_i(l_i+1)\}\) ?
arborescence 可以看成 intersection of two matroids
然而我们关于长度为\(L\)的路径的数量的约束却并不是matroid. ground set 是一个 arborescence 森林中的边, 如果长度为\(L\)的路径数量小于等于\(A\), 选择的边集就是一个independent set. 这种描述不能满足 exchange property.
(本来还想通过说明即使只有一个路径数量约束也是 intersection of three matroids 来证明即使是arborescence这个问题也是NP-Hard…不过就算成立也不能这样说明.)
1.2 也许 greedy 可行
把约束按照\(L_i\)从大到小排序, 对于一个长度是\(L_i\)的路径数量是\(a_i\)条这样的约束, 构造这样一个有向树:
O -> O -> ... -> O -> O
\-> O \-> O
|-> O |-> O
... ...在\(L_i\)对应的深度的顶点插入合适数量的儿子.
然后根据构造出的有向树中长度为更小的 \(L_j\) 的路径的数量并修改 \(a_j\).
换一种描述方法: 假设根的深度是0. 用一个pair\((L_i, A_i)\)来表示一个路径数量的约束(长度为\(L_i\)的路径有\(A_i\)条), 把这些pair按照 \(L_i\) 的降序排序. 最优解的树形图形状像上面画的一样, 深度为\(L_1\), 所有深度为\(p\)的顶点都是同一个深度为\(p-1\)的顶点的子节点. 深度为\(L_1\)的节点有\(A_1\)个, 深度为\(L_i(i\geq 2)\) 的顶点有 \(A_i-A_{i-1}+L_i-L_{i-1}+1\) 个.
只有一个路径数量约束(长度为\(L\)的路径数量是\(A\)), \(|V|=L+A\)
观察到对于\(k\)个路径约束, 使用的点数总共是
\[ \begin{align*} |V|&=L_1+A_1+\sum_{i=2}^N A_i-A_{i-1}+L_i-L_{i-1}\\ &= A_N+L_N \end{align*} \]
也可以验证这样的构造恰好满足长度为\(L_i\)的路径有\(A_i\)条.
2 DAG
不允许重边存在.
arborescence 情况下的贪心不再成立了, 比如这样的图: 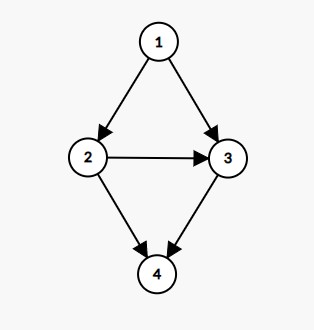
有向树的情况下是4个点是形成不了4条长度为2的路径的.
2.1 \(n\) 个点的DAG形成的长度为 \(L\) 的路径数量?
就是一个把能连接的边全部连接上的DAG吧。
路径数量就是组合数, \(f(n,L)\) 表示 \(n\) 个点的DAG形成的长度为 \(L\) 的路径数量, 看起来可能要找递推关系用生成函数算了, 但是实际上 \(f(n,L)\) 相当于 在 \([n]\) 当中包含 \(L\) 个元素的子集的个数, 给这个DAG拓扑排序, 所有可能的路径都是序列 \(\{1,2,...,n\}\) 的所有子序列, 数量也就是包含 \(L\) 个元素的子集个数. generatingfunctionology 1.5 是用生成函数算组合数的例子.
然后考虑一下连接了所有 \(n(n-1)/2\) 条边的DAG如果要保证长度为L的路径数量最多(仍然是 \(\binom{n}{L+1}\) ), 最多可以删除多少条边?
对于 \(n=4\) 的DAG和 \(L=2\) , 我们最多可以删掉一个边 \((1,4)\), 就是上面的图; 对于 \(L=3\) 就可以只保留 \((1,2), (2,3), (3,4)\) 了; \(L=1\) 一条边都不能删除.
可以删掉的边数只与 \(L\) 有关, 是 \(L(L-1)/2\) (\(i\) 和 \(j\) 不能相邻的条件是 \(n-(j-i+1)\leq L-2\))
目前还没有想到接下来该怎么办…