tropical bases and matroid circuits

http://matroidunion.org/?p=5403

In the post the author describes an interesting problem,

Problem Given a matroid $M=(E,\mathcal{I})$, find a minimal set of circuits that defines the matroid

The way he consider this problem is not by looking at the circuits but the flats. Any circuit excludes some sets from being flats. If we are given a circuit $c$, any set $A$ that contains $|c|-1$ elements of $c$ can not be a flat of $M$. So the idea is to find a minimal set of circuits that excludes all non-flat sets of $M$.

1 combinatorial definition

A circuit $c$ excludes a set $A$ if exactly one element of $c$ is not in $A$. A collection of circuits ${\mathcal{C}}^{\prime }\subseteq \mathcal{C}(M)$ is a tropical basis of $M$ if for every non-flat set $A$ there is a circuit $c\in {\mathcal{C}}^{\prime }$ that excludes $A$. The problem is then to find a minimal tropical basis of $M$.

2 algebraic geometry view

Tropical basis originally comes from algebraic geometry, see tropical geometry. The min tropical semiring is the semiring $(\mathbb{R}\cup \{+\infty \},\oplus ,\otimes )$, $x\oplus y=\min \{x,y\}$ and $x\otimes y=x+y$. The identity element for $\oplus$ is $+\infty$ and for $\otimes$ is $0$. The tropical variety of a tropical polynomial is the set of points where the polynomial achieves its minimum value at least twice.

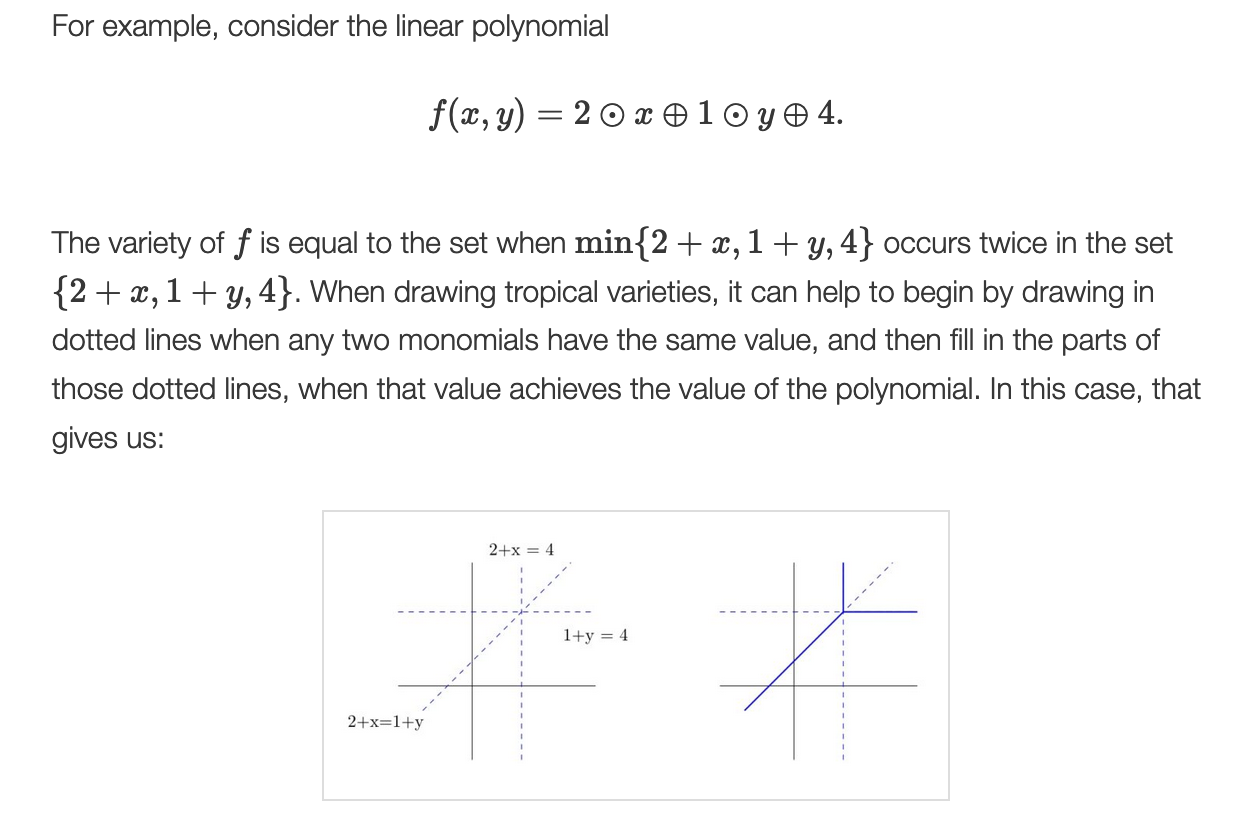
Tropical variety of a linear tropical polynomial is called tropical hyperplane.

For any set $A\subseteq E$ there is a natural representation of $A$ as a vector in $\{0,+\infty {\}}^{|E|}$, where the $i$-th coordinate is $0$ if $i\in A$ and $+\infty$ otherwise.(This is very similar to the indicator vector of a set in $\{0,1{\}}^n$. If the $i$-th element exists in the given set we put the identity element of $\otimes$ and otherwise the identity element of $\oplus$.) Then we can define a linear tropical polynomial associated with a circuit $c$ just like the dot product of two vectors in ${\mathbb{R}}^n$. For example consider a circuit $c=\{1,2,3\}$ in $U_{2,4}$, $f_c(x_1,x_2,x_3,x_4)=(0\otimes x_1)\oplus (0\otimes x_2)\oplus (0\otimes x_3)\oplus (+\infty \otimes x_4)$.

Denote the tropical hyperplane of a circuit $c$ by $T(c)$. $T(c)$ is the space of all vectors $v$ where $f_c(v)$ achieves its minimum at least twice. $T(\mathcal{C})={\bigcap }_{c\in \mathcal{C}}T(c)$ is the set of $v$ excluded by all circuits in $\mathcal{C}$. A set ${\mathcal{C}}^{\prime }\subseteq \mathcal{C}(M)$ is a tropical basis for matroid $M$ if $T({\mathcal{C}}^{\prime })=T(\mathcal{C})$.

3 connections between the two definitions

Combinatorial definition. ${\mathcal{C}}^{\prime }\subseteq \mathcal{C}$ is a tropical basis if for every non-flat set $A$ there is a circuit $c\in {\mathcal{C}}^{\prime }$ that excludes $A$.

Algebraic definition. ${\mathcal{C}}^{\prime }\subseteq \mathcal{C}$ is a tropical basis if $T({\mathcal{C}}^{\prime })=T(\mathcal{C})$.

Lemma For any ${\mathcal{C}}^{\prime }\subseteq \mathcal{C}$, $T({\mathcal{C}}^{\prime })=T(\mathcal{C})$ if and only if $T({\mathcal{C}}^{\prime })\cap \{0,1{\}}^n=T(\mathcal{C})\cap \{0,1{\}}^n$

This lemma shows that we can only consider the indicator vectors when dealing with the algebraic definition.

Note that $\mathcal{C}$ excludes all non-flat sets of $M$. Thus our combinatorial definition is equivalent to ${\mathcal{C}}^{\prime }$ excluding the same sets as $\mathcal{C}$. Let $\overline{T}(c)$ be the collection of sets which are not excluded by $C$. Then ${\mathcal{C}}^{\prime }$ is a tropical basis if and only if $\overline{T}({\mathcal{C}}^{\prime })=\overline{T}(\mathcal{C})$. Now we consider the algebraic definition. One can see that for any non-loop circuit $c$ and set $A$, $A\notin T(c)$(in other words, $f_c(A)$ achieves its minimum only once), if and only if $c$ excludes $A$. Thus $T(\mathcal{C})$ is the collection of all sets that are not excluded by any of the circuits in $\mathcal{C}$. Now it is easy to see that these two definitions are equivalent.

current status It seems that Bergman fan of a matroid is related to this topic. https://arxiv.org/abs/math/0411260 This seems to be a bridge between matroid theory and algebraic geometry. June Huh’s work is also related to this topic. https://arxiv.org/abs/1104.2519