Vertex and Edge Connectivity Interdiction

Posted on February 13, 2025 by Yu Cong
Tags: , ,
As a natural generalization of min-cut, the following problem seems interesting to me,
Problem1

Given a graph \(G=(V,E)\) and an integer \(k\), find the minimum edge set whose removal breaks \(k\)-vertex connectivity?

Alternatively, one can consider a closely related version of Problem 1,
Problem2

Given a graph \(G=(V,E)\) and an integer \(k\), find an edge set \(F\subset E\) with size at most \(k\) whose removal minimizes the vertex connectivity of \(G-F\).

This problem can be called the “vertex connectivity interdiction”. One can also consider the “algebraic connectivity interdiction” (the second smallest eigen value of the Laplacian matrix).

In fact, I think Problem 2 is not well motivated. I am interested in it since there may be connections between breaking vertex connectivity and breaking combinatorial rigidity. However, it seems strange to consider interdiction problems on edge set for vertex connectivity. For vertex removal, this problem is easy (by splitting vertex and finding mincut).

1 Checking \(k\)-vertex connectivity

Checking if a given graph is \(k\)-vertex connected can be done in polynomial time. By Menger’s theorem we need to check if for every vertex pair \((s,t)\) there are at least \(k\) vertex disjoint paths (excluding \(s\) and \(t\)) connecting \(s\) and \(t\). The number of vertex disjoint paths between \(s\) and \(t\) can be easily computed through max flow. We replace every internal vertex \(v\) with two copies \(v_{in}\) and \(v_{out}\) and add directed edges from \(N(v)\) to \(v_{in}\) and from \(v_{out}\) to \(N(v)\) with capacity 1. The integral max flow is the number of internally disjoint paths between \(s\) and \(t\). Since the constraint matrix of flow problems is TU, maximizing the flow gives us the vertex connectivity.

Instead of computing the flow for every pair, if we want one flow that gets the demand for every vertex pair \((i<j)\), the problem becomes much harder. This is Multi-commodity flow problem.

Currently the fastest algorithm for computing vertex connectivity is [1] https://dl.acm.org/doi/10.1145/3406325.3451088. There is a nice table for a summary of connectivity related algorithms.
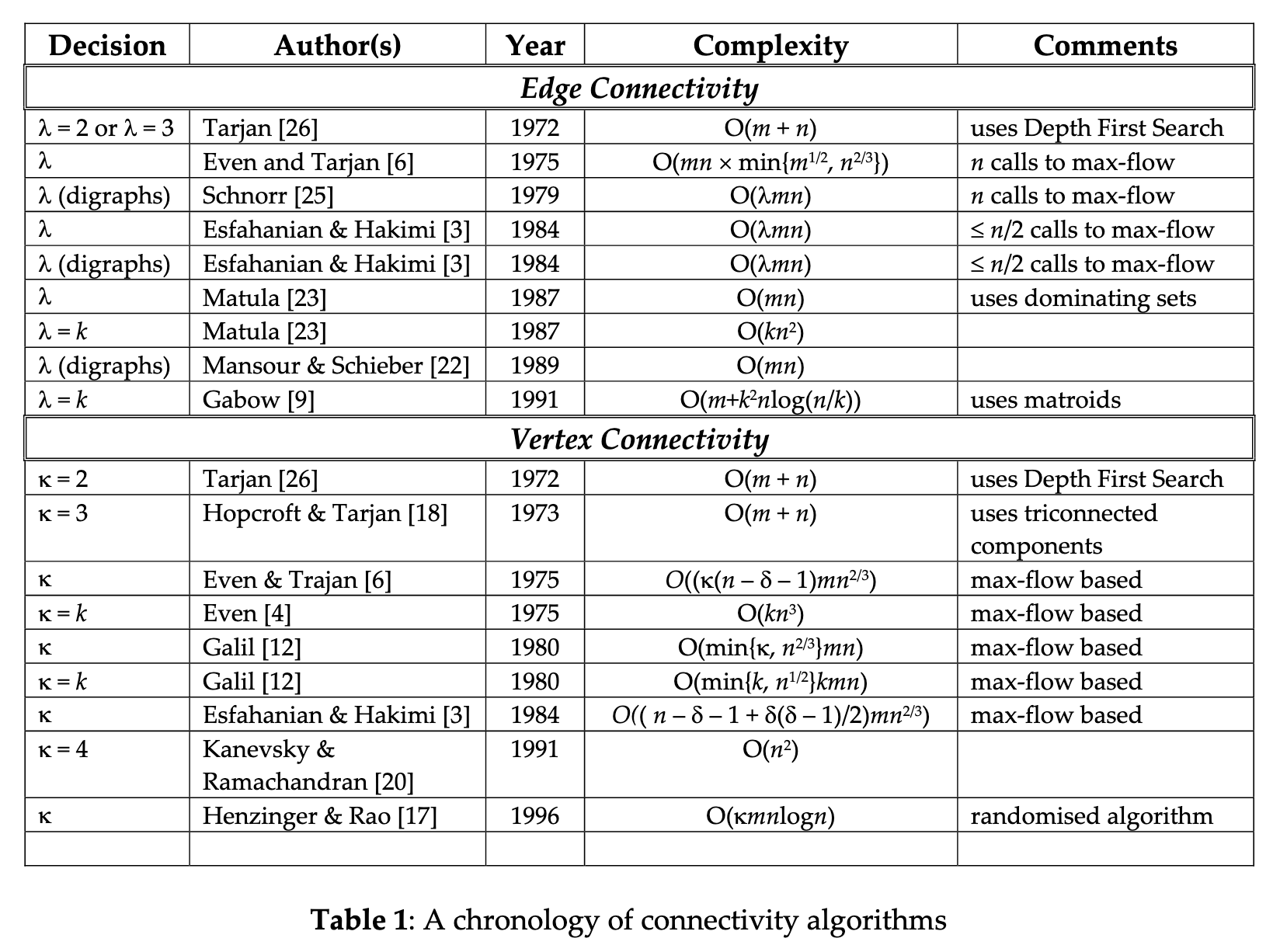
image courtesy of Abdol–Hossein Esfahanian. link

[1] appears in the last line. The conference version was published on FOCS96.

1.1 Minimum cut for edge connectivity

Finding the minimum edge set whose removal breaks the \(k\)-edge connectivity is “easy”. It is known that the global min-cut is the edge connectivity number. Thus we can simply compute the min-cut and remove any number of the edges as needed. — which is not true! For unit edge weights this problem is indeed that easy. However, for general weights edge-connectivity cut is not as easy as min-cut. This problem is actually the unit cost version of connectivity interdiction. See next section for more details.

1.2 Minimum cut for vertex connectivity

With the knowledge of how to compute vertex connectivity, we try to compute the minimum cut for \(k\)-vertex connectivity in a similar way. First we can find the vertex pair \((s,t)\) with the smallest number of internally disjoint paths. Note that we are dealing with the modified graph when computing the vertex connectivity number with flow. Hence the min-cut may contain edges that are not in the original graph, i.e., the edges connecting \(v_{in}\) and \(v_{out}\). For example, consider a graph where every edge has multiplicities 2. The min-cut reported by the flow algorithm should only contain edges between \(v_{in}\) and \(v_{out}\).

There is a list of open problems on vertex(node) connectivity. I guess Problem 1 is NP-hard but cannot prove it. However, the capacitated version of Problem 2 and Problem 1 is hard. Given a graph \(G=(V,E)\) and edge weights \(w:E\to \Z_{\geq 0}\) and costs \(c:E\to \Z_{\geq 0}\) and a budget \(b\geq 0\), find edge set \(F\subset E\) such that \(c(F)\leq b\) and such that removing \(F\) minimizes the vertex connectivity of \(G-F\). Similar to the edge connectivity case (which will be shown in the next section), if the cost \(c\) is nontrivial then kanpsack is a special case of this problem. (Consider \(G=K_n\) for some large \(k\). Pick a \(K_{n-1}\) in \(G\) and set the cost of edges in \(K_{n-1}\) to infinity.) How hard is Problem 2 if costs are trivial?

2 (Edge) Connectivity interdiction

If we replace the vertex connectivity in Problem 2 with edge connectivity, then the problem is called connectivity interdiction and was first studied by Zenklusen [2].
Problem3

Given a graph \(G=(V,E)\) and costs \(c:E\to \Z_+\) and weights \(w:E\to \Z_+\) and a budget \(B\in \Z_+\), find the edge set \(R\) such that \(c(R)\leq B\) and that minimizes the \(w\)-weighted min cut in \((V,E\setminus R)\).

The Fault-Tolerant Path problem (FTP) seems sililar to Problem 3. In FTP problem, we are given a edge-weighted directed graph \(G=(V,E)\), a subset \(U \subseteq E\) of vulnerable edges, two vertices \(s,t\in V\) and integers \(k\) and \(\ell\). The task is to decide whether there exists a subgraph \(H\) of \(G\) with total cost at most \(ℓ\) such that, after the removal of any \(k\) vulnerable edges, \(H\) still contains an \(s\)-\(t\)-path. The problem degenerates into finding \(k\)-edge connected spanning subgraph if the set of vulnerable edges is \(E\).

A recent paper [3] gives an FPTAS for the problem. Here I try to develop the intuition since I have never seen an algorithm based on reweighting edges this complicated and ingenious.

First one can see that the optimal solution can always be a subset of edges in a cut of \(G\). This is because if the optimal solution \(R^*\) contains any edge not in the cut, we can safely delete it from \(R^*\). Thus the optimal solution is indeed a pair \((C^*,R^*\subset C^*)\). The authors call this problem the \(b\)-free min-cut problem (\(b\) is the budget and we are allowed to pick edges for free in the “mincut” with total weight at most \(b\)).

So the goal is to find a FPTAS for the \(b\)-free mincut problem. The problem is hard since it contains knapsack as a special case. (Consider a graph with many parallel edges and only 2 vertices.) However, it is known that there is a FPTAS for knapsack. If we know part of the optimal solution, i.e., \(C^*\), we can use the FPTAS for knapsack to find the optimal \(R^*\).

At this stage, if there is a hint suggesting reweighting the edges, I would guess that \(C^*\) is exactly (or close to) the min-cut of the re-weighted graph. Based on this idea I would also guess that, although the connectivity interdiction problem (\(b\)-free min-cut) is NP-hard, \(C^*\) can be computed in polynomial time. In other words, the intractable part is solving the knapsack in \(C^*\). This statement seems reasonable, since this problem is know to be in P for unit costs and in that case the kanpsack is trivial. Let’s assume that my guess is correct and work on the reweighting part.

2.1 Reweighting

There is a chapter on reweighting in Sariel Har-Peled’s gemetric approximation book(not quite the same as the reweighting technique in [3]). Is reweighting a common technique for designing approximation algorithms?

One possible weight function is setting \(w(e)=0\) for all \(e\in R^*\)… However, this is cheating since we assume that \(R^*\) is the hard part. So now we need to find a weight function such that the following holds,
  1. The min-cut of the re-weighted graph is close to \(C^*\).
  2. Computing the weight function takes polynomial time.

From the “cheating” example we can see that knowing \(R^*\) does help but computing \(R^*\) is hard. So maybe we can find a slightly worse weight function which is a lot easier to compute. So it seems like we are making a trade-off between how close the global min-cut of the re-weighted graph is to \(C^*\), and how much time is needed to compute this weight function. This paper indeed does a great job in finding such a balance. I sent an email to one of the authors to ask for the intuition behind the reweighting but did not get a real answer. They suggested reading [2]. Zenklusen did almost the same thought experiment as above. Instead of using reweighting, he indirectly enumerated \(R^*\). Consider the unit cost case for example. If the optimal cut \(C^*\) is given, the interdicted edges \(R^*\) will be those \(b\) edges in \(C^*\) with heaviest weights. We cannot directly enumerate \(R^*\) since it still takes exponential time. What we can enumerate is a lowerbound of the weight of edges in \(R^*\). Set all edges with weights exceeding this lowerbound to be in \(R^*\) and find global min-cut with additional budget constraint on these edges. Then we have only \(m\) lowerbound to enumerate and the budgeted min-cut can be computed fast. For general costs, he enumerated the set of \({1}/{\varepsilon}\) edges with heaviest weights in \(C^*\).

The plan is to figure out how did the authors come up with the weight function in [3] and if it is possible to find a better weight function.

The key part is the following new problem called normilized min-cut,
Problem4Normalized min-cut

Given a problem instance of connectivity interdiction, find a cut \(C\) and its subset \(F\subset C\) s.t. \(0\leq c(F)\leq b\) and \(\frac{w(C\setminus F)}{b+1-c(F)}\) is minimized.

I have been thinking for a while how this problem is involved but have no clue. However, it does work… The weight function is defined based on an estimation of Problem 4. The authors claim that the optimal solution to b-free min-cut problem is a 2-approximate min-cut of the reweighted graph. Then they enumerate all 2-approximate min-cut of the reweighted graph and use the FPTAS alg for knapsack on each cut to find a \((1+\epsilon)\)-approx solution.

2.2 More on normalized min-cut

If one slightly modifies lemmas in section 2 in [3], there are some interesting properties. Let \(\tau\) be the value of the optimal normalized min-cut (in [3] \(\tau\) is an estimation of the optimum) and define \(\tilde{w}_\tau\) accordingly. Then one can prove that the global min cut in \((G,\tilde{w}_\tau)\) is exactly the optimal cut in the normalized min-cut of \((G,w)\) (slightly modify lemma3 to see this). Also the value of min-cut in \((G,\tilde{w}_\tau)\) is \(\tau(b+1)\).

For unit cost, the optimum of normalized min-cut can be computed using the same complexity as connectivity interdiction (ignoring polylog factors) [4]. Consider the sequence \(\set{\lambda_i=\frac{\min_{|F|\le i} w(C\setminus F)}{b+1-i}}\). If this is unimodal, \(O(\log b)\) calls of connectivity interdiction algorithm should be sufficient. (Note that \(b\) is at most \(m\) since costs are unit.) However, one can easily see that this sequence is not unimodal. Thus I don’t quite believe this claim.
Comments on [3]

After reading [4], I finally know why the authors use Problem 4 to solve connectivity interdiction. Almost all techniques they used are directly from [4]. Read section 2 of [4] until 2.2, you know almost everything needed for a FPTAS solving connectivity interdiction. In fact, the authors cite [4] in their paper,

In a recent paper of Chalermsook et el. [CHN+22] on survivable network design, the same problem was first introduced (under a different name “minimum normalized free cut”) to deal with a certain boxing constraint in the LPs. There, a special case of unit-edge costs is actually solved as a technical necessity. To obtain an FPTAS in this paper, we emphasize that we do not need to solve the normalized min-cut problem per se, but rather we use its optimal solution as a certificate in the analysis of the weight function \(\tilde{w}(i)\) in Theorem 3.

This paragraph is somewhat misleading. There is no clearly indication that very similar (in fact, almost identical) results are proven [CHN+22].

It was mentioned in a footnote of [4] that a general version of normalized min-cut is used in this paper, which in turn mentioned that normalized min-cut is an ordinary subroutine in MWU frameworks.

some notes here

References

[1]
M.R. Henzinger, S. Rao, H.N. Gabow, Computing vertex connectivity: New bounds from old techniques, Journal of Algorithms. 34 (2000) 222–250 https://doi.org/10.1006/jagm.1999.1055.
[2]
R. Zenklusen, Connectivity interdiction, Operations Research Letters. 42 (2014) 450–454 10.1016/j.orl.2014.07.010.
[3]
C.-C. Huang, N. Obscura Acosta, S. Yingchareonthawornchai, An FPTAS for Connectivity Interdiction, in: Integer Programming and Combinatorial Optimization, Springer Nature Switzerland, Cham, 2024: pp. 210–223 10.1007/978-3-031-59835-7_16.
[4]
P. Chalermsook, C.-C. Huang, D. Nanongkai, T. Saranurak, P. Sukprasert, S. Yingchareonthawornchai, Approximating k-Edge-Connected Spanning Subgraphs via a Near-Linear Time LP Solver, in: 49th International Colloquium on Automata, Languages, and Programming (ICALP 2022), Schloss Dagstuhl – Leibniz-Zentrum für Informatik, Dagstuhl, Germany, 2022: pp. 37:1–37:20 10.4230/LIPIcs.ICALP.2022.37.