0.1 duality between point and line
二维平面上有一条直线\(y=ax-b\)和一个点\((c,d)\)，现在我想描述一下点和直线之间的相对位置； 点如果在直线上面，说明\(x=c\)的时候直线取得的\(y\)小于\(d\), 也就是说\(d>ac-b\)，这里也可以将 \(c,d\)看成系数，\(a,b\)当成带入的坐标，表示的意思变成\((a,b)\)这个点位于直线\(y=cx-d\)的上面0.2 upper envelope of linear functions
现在二维平面上有很多条直线，我想找到最上面的边缘线(upper envelope)
0.3 k-level
k-level 是推广的 upper envelope，找的是最上面的 k 条直线(实际上定义是下方正好有 k 条直线的那个边缘线)， 也就是需要找到正好上方有 k-1 条直线的那个边缘线。这个边缘线上的点上方应该有恰好 k-1 条直线， 下方有 n-k 条直线。类似 upper envelope 的处理，研究和直线互为对偶的点。要找的是一个类似凸包下边缘的东西 上的点，这些点对应的直线就是能够出现在 k-level 边缘线上的那些直线。 下面是 1999 Timothy M. Chan 中的算法 首先容易的方法是枚举所有直线的交点\(O(n^2)\)，然后对这些交点分出的所有区间计算最大的 k 个直线（应该是\(O(n^3)\)， \(n^2\)个区间，每个区间用 median of medians 线性时间找到 top k） 1999 Timothy M. Chan 的思路是从左到右扫描 x 轴，维护两个优先队列，一个维护在当前的 x rank 小于 k 的直线是哪些，一个维护大于等于 k 的是哪些。如果把 横轴 x 看成时间，优先队列在维护一些会在一维直线上做匀速运动的点，这种东西叫做 kinetic data structure，实现方法先不讨论 有了这种数据结构之后就可以按照这样的步骤维护 k-level: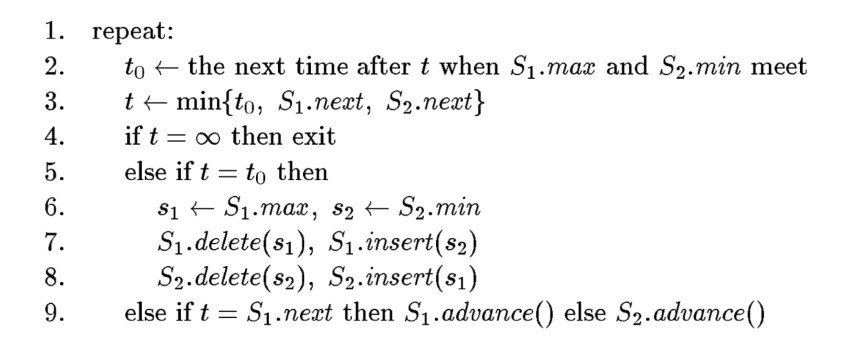
0.3.1 目前 kinetic priority queue 的复杂度
kinetic priority queue 需要实现的操作： - 插入点 - 删除点 - advance（把时间往后推） - 维护最小值 文中讨论复杂度基于两个上界：优先队列中点的数量的上界\(n\)，插入操作的数量上界\(m\)
Observation12.1
For elements moving linearly, the number of times S.min changes is \(O(m\alpha(n))\).
实际上 kinetic priority queue 在维护的是一个子集的 lower envelope，lower
envelope 上的 breakpoint 数量有 上限\(O(m\alpha(m))\)（来源见 1999
Timothy M. Chan）(这个奇怪复杂度是怎么来的？zh.wikipedia,
en.wikipedia
lower envelope 上的线段编号写成一个序列就 是这个 Davenport–Schinzel
sequence)
实际上这个界对于直线是非常不紧的，线段才可能产生长度为 4
的交替子序列，直线只能产生长度为 2 的；所以线段是 3 阶 DS sequence 而
直线是 1 阶，从对偶对应的凸包也可以看出 breakpoint 上限是\(O(n)\)，所以文章这里考虑的是带上插入删除操作的
使用暴力方法，复杂度\(T(n,m)=O(mn\alpha(n))\)
复杂度这里实际上算的是从一个空的 KPQ
开始，插入点，删除点，advance，按照需要进行操作，直到\(t=\inf\)花费的时间； Observation 给出了
advance 操作的数量上限，每次 advance 必然发生\(S.min\)改变。插入和删除操作数量上界是\(m\)。
文章中用分治，把每个 kinetic priority queue \(S\)维护的集合分成\(r\)组，每组用一个 kinetic priority queue
维护(\(P\in S.\Pi\))，
然后再用一个额外的 kinetic priority queue \(S.Q\)维护这 r 个子队列最小值的最小值
KPQ \(S\)
只需要暴露出上面说的四种操作，首先\(S.maintain(),S.advance()\)如下，很好理解
0.3.1.1 \(N(n,m)\)
\(N(n,m)\)表示递归方法中一个 KPQ 做 advance 操作的数量 \[N(n,m)=\sum_{i=1}^r N(n/r,m_i)+O(m\alpha(n))\] 其中\(\sum m_i=m\)（所有插入次数被分配到了每个子队列中） \[N(n,m)=O(\alpha(n) m\log_r n)\]复杂度： \[T(n,m)=\sum_{i=1}^r T(n/r,m_i)+O(m\alpha(n)\log n+mr\alpha(n))\] RHS 第二项需要解释，\(O(m\alpha(n)\log n+mr\alpha(n))\)完全是上面\(S\)和\(S.Q\)维护产生的复杂度， 现在文章认为\(S.Q\)使用暴力方法，插入删除操作复杂度都是\(O(S.Q.size)\)，\(S.advance()\)A5 说明每次\(S\)的最小值改变 \(S.Q\)都会进行一次插入和一次删除，所以\(S.advance()\)就会让\(S.Q\)产生\(O(m\alpha(n))\)次插入和删除，每次\(O(r)\)， 这部分复杂度就是\(mr\alpha(n)\)（因为 n 小于 m，队列中的元素数量肯定小于插入次数，\(S.insert()\)执行次数一定少于 \(O(m\alpha(n))\)，这里不用继续考虑 D5 和 I5 操作了）；其次是 A1 和 M2 中找\(P.next\)最小的 P，单独用一个大小为 r 的堆来 维护这个信息，回答 A1 和 M2 是常数时间，但是每次任意一个\(P.min\)发生改变或者发生插入删除的时候都要\(\log r\)时间维护， 需要\(O(N(n,m)\log r)=O(m\alpha(n)\log n)\)，令\(r=\lceil \log n\rceil\) \[T(n,m)=O(m\alpha(n)\log^2 n/\log \log n)\] 这种递归方法我写了代码 github 感觉写的有点丑陋，而且用的是 boost 的 heap最后得到\(\sum_{i=1}^{\log_r n} \alpha(\frac{n}{r^{i-1}})*m\) sum 里面直接取最大值，可以得到上面的结果
层数 个数 sum 1 1 \(m\alpha(n)\) 2 r \(m\alpha(\frac{n}{r})\) 3 \(r^2\)(r个一组，一共r组) \(m\alpha(\frac{n}{r^2})\) … … … \(\log_r n\) \(n/r\) \(m\alpha(1)\)
0.3.2 优化
需要用到 semi dynamic convex hull （只支持删除操作的动态凸包）， 去查了一下发现很多有趣的结果， - Kirkpatrick and Seidel 把二维平面凸包做到\(O(n\log k)\) n 是输入大小，k 是输出大小。 - 完全动态的凸包（支持插入和删除）Overmars 做到了\(O(\log^2 n)\) - semi dynamic convex hull 仅插入单次操作可以做到单次\(O(\log n)\)，仅删除可以做到单次均摊\(O(\log n)\)先不讨论 semi dynamic convex hull 的实现，如果已经有了一个维护删除操作下的凸包的数据结构，如何实现一个仅支持删除操作的 KPQ？ 首先如果是仅删除的 KPQ，寻找最小值实际上就是在一些都从左端点在 x=0、右端点位置不同的线段组成的 lower envelope， 同样根据上面的 DS sequence ， 可以看出两个线段组成最长交替子序列长度是 3，是一个 2 阶 DS sequence，得知\(advance()\) 次数上界也是\(O(n)\) 那么我们可以先算出最开始的 lower envelope（一个凸包，\(O(n\log n)\)）然后再用 semi dynamic convex hull 去维护 删除操作，n 个删除操作只需要\(O(n\log n)\) 于是借用上面定义的衡量 KPQ 的复杂度\(T(n)=O(n\log n)\) 这种方法先不写了，我认为我能把它成功写出的概率不大，而且过于复杂。首先上面说的 semi dynamic convex hull 只能做到只处理插入操作和只处理删除操作， 得到的 kinetic priority queue 也是只能支持一种操作， 1980 Bentley & Saxe 发明了用一种叫做 binary-counting 的技巧把只支持一种操作的数据结构变成支持插入和删除的，维护的时间加一个\(\log\)； 为了消除掉这个\(\log\)还需要使用 b-ary。 最终复杂度能达到\(O(n\log m+m\log^{1+\epsilon}n)\)
0.3.3 随机化版本
AGARWAL et al. 对于\(\mathbb{R}^d\)上的 k-level[1] 证明了复杂度是\(\Theta(n^{\lfloor d/2 \rfloor}k^{\lceil d/2 \rceil})\)，上面链接中二维平面 k-level 复杂度 是\(O(nk + n\alpha(n) \log n )\) 应该在到目前为止随机化算法中 worst case 是最优的 upd Sep 2024. https://tmc.web.engr.illinois.edu/pub_kset.html 有很多 k-level 相关的问题和算法.References
[1]
K.L. Clarkson, Applications of random sampling
in computational geometry, II, in: Proceedings of the Fourth Annual
Symposium on Computational Geometry - SCG ’88, ACM Press,
Urbana-Champaign, Illinois, United States, 1988: pp. 1–11 10.1145/73393.73394.