好长的标题啊二维平面上有一些点 \(E\), 分成两组 \(B\) 和 \(E\backslash B\). \(\forall b\in B, \forall c\in E\backslash B\), find the largest slope of the segment \(bc\). 这个问题是在解决 parametric matroid optimization 的时候遇到的， 但是用这种方法得到的东西甚至没有最显然的办法快.
1 parametric matroid optimization
问题大概是这样 \[ \begin{aligned} \max_x \quad & (v-\lambda c)\cdot x\\ s.t. \quad x(S)&\leq r(S) &\forall S\subseteq E\\ x(E)&=p\\ x&\geq 0 \end{aligned} \] 有一个 matroid \(M\), ground set 是 \(E\), rank 是 \(p\), 每个 element 的权重是一个线性函数， 随着 \(\lambda\) 变化， 我们想要找到随着 \(\lambda\) 变化的这个线性规划的最优解的函数 \(\tau\). 首先这个 \(\tau\) 一定是 piecewise linear convex function. 这是因为所有的约束都是线性的(虽然可能数量是 ground set 大小的指数函数), \(x\) 的范围是一个凸多面体， 凸多面体顶点的 \(x\) 全部拿出来， 我们会得到一个候选的直线的集合， 然后实际上我们在这些直线里面取 max, 找的是平面上直线的 upper envelope, \(\tau\) 一定是 piecewise linear convex function. 然后关于\(\tau\)上面的 breakpoints 数量还有一个很好的性质. 数量是 \(\Theta(mp^{1/3})\), 这个是 Improved Bounds for Planar k -Sets and Related Problems 文章里证明的. (\(m=\|E\|\)) 然后问题是怎么找到\(\tau\).1.1 uniform matroid
uniform matroid 就是所有大小小于等于 \(p\) 的 \(E\) 的子集都是独立的. uniform matroid 的特殊情况下， 这个问题就变成一个叫做 k-level 的问题. 从上面的规划也能看出来， 相当于对于所有\(\lambda\)我们都找纵坐标最大的 \(p\) 条直线. 这个有超快的算法. Chan, T. M. (1999). “Remarks on k-level algorithms in the plane”. Archived from the original on 2010-11-04. 然后我写了文章里一个比较慢的用 kinetic heap 的版本 github1.2 graphic matroid
graphic matroid 的 ground set 是一个无向图里面的边集， ground set 的任何子集，只要在图里不成环就是独立的. 他的基也就是任何生成树. graphic matroid 情况下的\(\tau\) 也有超快的算法. https://link.springer.com/article/10.1007/PL00009396 关于这两种特殊的 matroid 情况下 \(\tau\) 上面的 breakpoints 数量有这样一个表.| “beakpoints” | lowerbound | upperbound | ref |
|---|---|---|---|
| k-level | \(\Omega(nc^{\sqrt{\log k}})\) for some constant c | \(O(n k^{1/3})\) | https://en.wikipedia.org/wiki/K-set_(geometry) |
| spanning tree | \(\Omega(m\alpha(n))\) graph with m edges and n vertices | the same as general matroid | https://link.springer.com/article/10.1007/PL00009396 |
| general matroid(number of different minimum weight bases) | \(\Omega(nr^{1/3})\) | \(O(nr^{1/3})\) | lb: https://link.springer.com/article/10.1007/PL00009396 ub: https://link.springer.com/article/10.1007/PL00009354 |
2 geometric view
我最开始想， 我可以想办法按照\(\lambda\)递增的顺序把 \(\tau\) 上面所有 breakpoints 都找到. 假设我们现在的 \(\lambda=\lambda_1\), 当前在\(\lambda_1\)我们也知道选择的 optimum base 是什么. 我们要找 base 里的直线和 base 外面的直线的大于\(\lambda_1\)的最小交点坐标. 也就是 \[ \begin{aligned} \min \quad (b-d)/(c-a)\\ s.t. \quad \{y=a\lambda+b\}&\in B \\ \{y=c\lambda+d\}&\in E\backslash B\\ (b-d)/(c-a)&\geq \lambda_1 \end{aligned} \] 我们找到下一个 \(\lambda\) 之后要看 matroid base 是否改变. 上面这个优化问题只是找到 base 和 不是 base 的直线的下一个交点， 但是他们交换了未必 optimum base 就会变. 下面有两个问题: 1. 快速找到下一个 \(\lambda\) 2. 我们找的 \(\lambda\) 有多少个？ 其实到这里已经该意识到这个思路可能有问题了. 但是我反而觉得我这个办法超过了上面 kinetic spanning tree(graphic matroid)的文章…3 find the next breakpoint
相当于在二维平面里有两组点， 找点之间连线斜率最接近\(\lambda\)的点对. 通过改变\(b\)可以把约束改成\((b_i-b_j)/(a_i-a_j)\leq 0\), 再把所有点先对\(y=0\)做对称在对\(y=x\) 做对称， 就变成了无约束的\(\max (b'_i-b'_j)/(a'_i-a'_j)\) 如果只有一组点， 求连线斜率最大可以\(O(n\log n)\)的时间内算出， 因为有一个性质， 斜率最大的线段一定是在按 a 的大小排序之后相邻的两个点取到， 但是如果是两组点就没有了这个性质…3.1 trivial version
这是问组里打 acm 同学得知的. cdq 分治. \(O(n\log^2 n)\). 我问了打 acm 的同学， 可以使用叫做 cdq 分治的技巧. 把所有二维点（不管是哪一组）按照 a 的大小排序， 然后开始分治。 把所有点分成左右两部分数量相等的点，两个组分别记为 A 和 B，左侧的属于 A 组的点记为\(A_l\), 右侧 A 组记为\(A_r\), B 组也同样记为\(B_l,B_r\), 斜率最大的线段可能出现在 3 个地方：- \(A_l,B_l\)之间的连线
- \(A_r,B_r\)之间的连线
- \(A_l,B_r\) or \(A_r,B_l\) 之间的连线
3.2 complicated version…
观察上面 cdq 分治的过程， 发现我们总是在维护左半, 然而 M. H. Overmars and J. Van Leeuwen, “Maintenance of configurations in the plane,” Journal of Computer and System Sciences, vol. 23, no. 2, pp. 166–204, Oct. 1981, doi: 10.1016/0022-0000(81)90012-X. 当中 fully dynamic convex hull 的数据结构几乎是在做一样的事. 他的数据结构是一个平衡树套平衡树. 我们直接把他的数据结构拿过来， 把 base 中的点和不在 base 的点分开， 外层平衡树每个节点维护八个半凸包， 每次 delete 或者 insert 操作之后都要维护我们要求的 slope, 就可以在和动态凸包完全相同的时间内找出我们想要的下一个交点. 也就是\(O(\log^2 m)\). (我觉得应该没问题…) 2D fully dynamic convex hull notes-hackmd.io 然后我注意到 kinetic spanning tree 的文章每个 breakpoint 大概要花 \(O(n^{2/3}\log^{c}n)\), 那这个动态凸包的方法岂不是超快. 然而没有那么好的事…4 number of “breakpoint”s
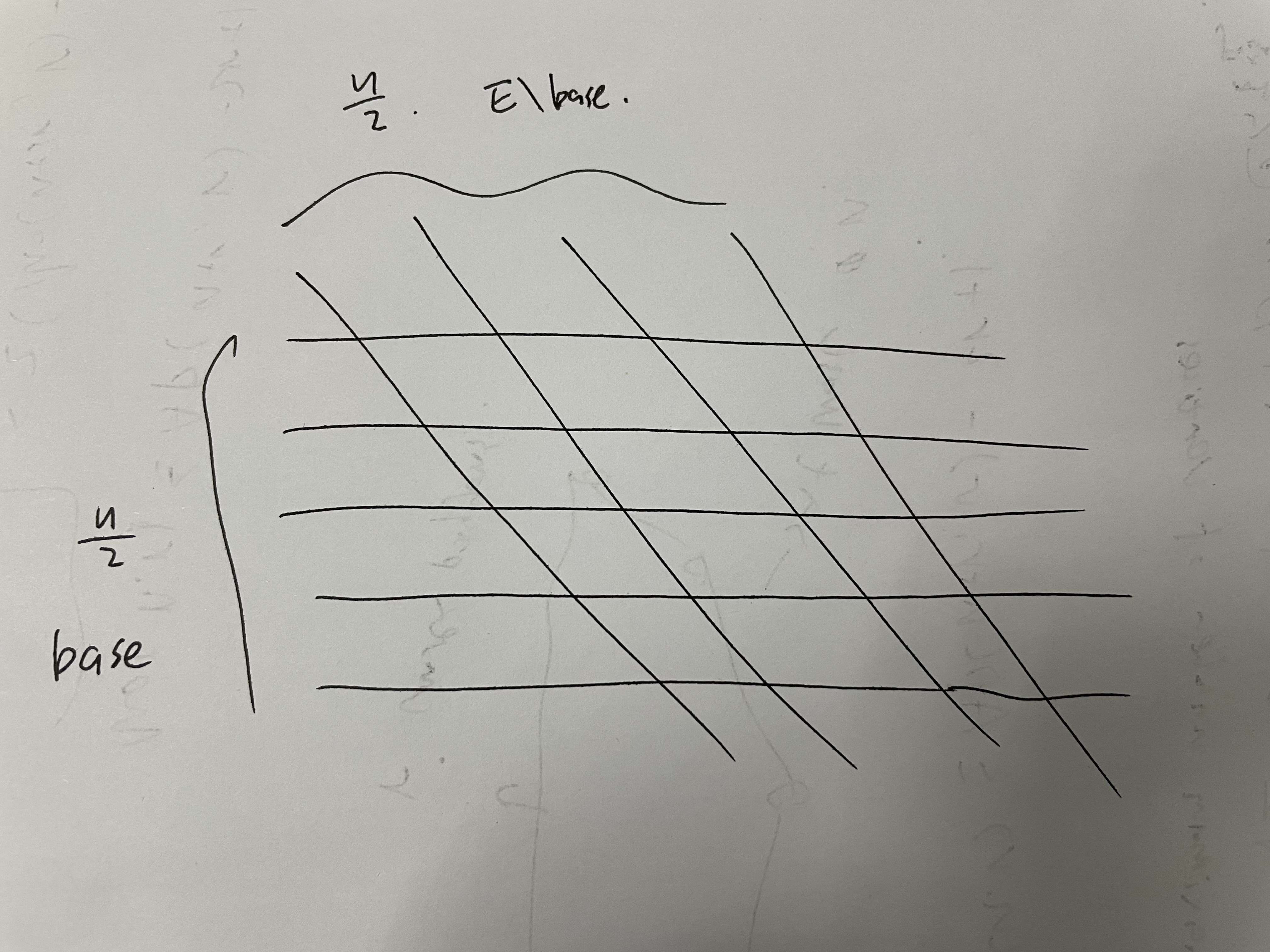
然而实际上我找的这个 “breakpoints” 的数量不是 \(O(k)=O(mp^{1/3})\), 而是 \(O(m^2)\). 上文说的 Improved Bounds for Planar k -Sets and Related Problems 文章里的证明用到叫做 Polygons in Arrangements 的问题(实际上是表格里 general matroid lowerbound 那个文章先提出来的) 看起来和我找 breakpoint 的过程非常相似. 我以为我的 “breakpoints” 的数量就是 \(O(k)\). 可以构造出一定会遇到 \(m^2/4\) 个 “breakpoints” 的 matroid 和直线. 比如