Median of medians & `std::nth

Tags: alg, C++

是一点 selection algorithm

支持随机查找的数组中找到第 k 大的元素是只需要线性时间. https://en.wikipedia.org/wiki/Median_of_medians

c++ 标准库里面也有类似的算法， std::nth_element

但是他没有返回值，而是把有 random access iterator 的容器的元素顺序改变了，保证比第 n 个元素大的都在第 n 个元素前面，第 n 个元素就是第 n 小的元素. 听起来过程和 median of medians 差不多一样，此时我还不知道 intro sort 这种东西… 于是准备写一个比 nth_element 更快的模板，有返回值，不改原来的序列的元素.

然后…成功成为小丑，维基百科的 median of medians 抄下来比标准库慢好多…

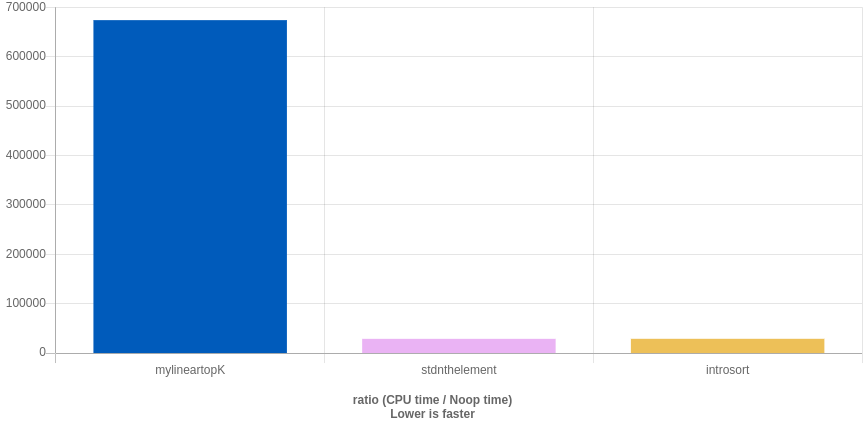
quickbenchmark

median of medians 是把元素五个一组(一个 5-tuple)找中位数，然后找到中位数的中位数(pivot). 现在有一半的 tuple 的中位数小于 pivot, 每个 tuple 都有五个元素，其中两个小于这个 tuple 的中位数，两个大于这个 tuple 的中位数. 这样我们就知道了，在 tuple 的中位数小于 pivot 的这些 tuple 里面，小于等于该 tuple 中位数的元素(每个 tuple 有三个这样的元素)都一定小于 pivot. 也就是说如果我们把\(\lceil \frac{n}{5} \rceil\)个 tuple 都按照他们的中位数大小关系排好序的话，排在 pivot 所在的 tuple 前面的这些 tuple 里面，有 60% 是一定比 pivot 小的，他们一定是前半个序列的前 60% 的元素，同理排在 pivot 所在 tuple 后面的所有 tuple, 每个都有三个元素比 pivot 大，他们一定位于后半序列的最后 60%, 我们每次至少可以扔掉50%*60%=30%的元素(这是最坏情况， pivot 所在 tuple 经过排序之后恰好在第一个或最后一个，实际上我们不排序！) 注意到选择 pivot 仍然是一个 select 过程，我们一样可以用这个 median of median 来做，非常巧妙

\[ T(n)=T(n/5)+T(0.7n)+O(n) \]

然后再来看看 introsort 是怎么做的

这是stl_algo.h的实现

  template<typename _RandomAccessIterator, typename _Size, typename _Compare>
    _GLIBCXX20_CONSTEXPR
    void
    __introselect(_RandomAccessIterator __first, _RandomAccessIterator __nth,
		  _RandomAccessIterator __last, _Size __depth_limit,
		  _Compare __comp)
    {
      while (__last - __first > 3)
	{
	  if (__depth_limit == 0)
	    {
	      std::__heap_select(__first, __nth + 1, __last, __comp);
	      // Place the nth largest element in its final position.
	      std::iter_swap(__first, __nth);
	      return;
	    }
	  --__depth_limit;
	  _RandomAccessIterator __cut =
	    std::__unguarded_partition_pivot(__first, __last, __comp);
	  if (__cut <= __nth)
	    __first = __cut;
	  else
	    __last = __cut;
	}
      std::__insertion_sort(__first, __last, __comp);
    }

introsort 基本上就是 quicksort 的 pivot 划分过程 +heap sort+insertion sort

但是 stl 是没有用插入排序的，而且很多地方在语言上做了优化. 基本上还是一样的.

首先在 list 比较大的时候递归调用 introsort, 首先用std::__unguarded_partition_pivot找个 pivot, 方法是直接取当前序列的正中间的元素作为 pivot. 然后根据要找的 nth_element 和 pivot 相比哪个大来修改下一步递归的区间.

在 list 比较小的时候就直接用 heap select, 这个函数是这样的:

  /// This is a helper function for the sort routines.
  template<typename _RandomAccessIterator, typename _Compare>
    _GLIBCXX20_CONSTEXPR
    void
    __heap_select(_RandomAccessIterator __first,
		  _RandomAccessIterator __middle,
		  _RandomAccessIterator __last, _Compare __comp)
    {
      std::__make_heap(__first, __middle, __comp);
      for (_RandomAccessIterator __i = __middle; __i < __last; ++__i)
	if (__comp(__i, __first))
	  std::__pop_heap(__first, __middle, __i, __comp);
    }

先建堆，然后满足条件就pop

make_heap

  template<typename _RandomAccessIterator, typename _Compare>
    _GLIBCXX20_CONSTEXPR
    void
    __make_heap(_RandomAccessIterator __first, _RandomAccessIterator __last,
		_Compare& __comp)
    {
      typedef typename iterator_traits<_RandomAccessIterator>::value_type
	  _ValueType;
      typedef typename iterator_traits<_RandomAccessIterator>::difference_type
	  _DistanceType;

      if (__last - __first < 2)
	return;

      const _DistanceType __len = __last - __first;
      _DistanceType __parent = (__len - 2) / 2;
      while (true)
	{
	  _ValueType __value = _GLIBCXX_MOVE(*(__first + __parent));
	  std::__adjust_heap(__first, __parent, __len, _GLIBCXX_MOVE(__value),
			     __comp);
	  if (__parent == 0)
	    return;
	  __parent--;
	}
    }

_GLIBCXX_MOVE std::move, 所有的临时变量都用右值引用存起来，少了很多复制操作

我好慢…

Median of medians & `std::nth_element`