看了这本书 The primal-dual method for approximation algorithms and its application to network design problems
1 intro
考虑一个线性规划问题
\[ \begin{align*} \min \quad &c^Tx\\ s.t. \quad Ax&\geq b\\ x&\geq 0 \end{align*} \]
他的对偶:
\[ \begin{align*} \max \quad &b^Ty\\ s.t. \quad A^Ty&\leq c\\ y&\geq 0 \end{align*} \]
根据原问题的kkt条件中的互补松弛条件(叫做对偶问题的互补松弛条件):
\[ y^T(Ax-b)=0 \]
同样根据对偶问题的kkt的互补松弛条件(叫做原问题的互补松弛条件),有
\[ x^T(A^Ty-c)=0 \]
primal dual方法首先有一个对偶问题的可行解\(y\),如果能找到一个原问题的可行解\(x\)满足互补松弛条件, 那么\(x\)和\(y\)就是原问题和对偶问题的最优解,但是\(y\)如果并非最优解,就找不到可行解\(x\)满足互补松弛条件。于是希望 引入一个新问题,最小化原问题可行解\(x\)对互补松弛条件的违反。首先引入下标集\(I= \{ i|y_i=0 \} ,J= \{j |A^jy=c \}\),其中 \(A_i\)表示\(A\)的第\(i\)行,\(A^j\)表示\(A\)的第\(j\)列(写成行向量),下面是restricted primal problems:
\[ \begin{align*} \min \quad \sum_{i\notin I} s_i&+\sum_{j\notin J} x_j \\ s.t. \quad Ax_i&\geq b_i & i\in I\\ \quad Ax_i-s_i&= b_i & i\notin I\\ x&\geq 0\\ s&\geq 0 \end{align*} \]
其中\(s_i(i\notin I)\)是对对偶问题的互补松弛条件的惩罚项,\(y_i\not ={0}\rightarrow A_ix=b_i\); \(x_j(j\notin J)\)是对原问题互补松弛条件的惩罚,\(A^jy\not ={c_j}\rightarrow x_j=0\);
如果restricted primal problem的最优解是0,那么说明找到了原问题的一个完全满足互补松弛条件的可行解\(x\),\(x\)和\(y\)应该是原问题和对偶问题的最优解; 如果最优解不是0,说明\(y\)并非最优解,需要改进(在例子中需要变大)。我们首先考虑restricted primal problem的对偶:
\[ \begin{align*} \max \quad &b^Ty'\\ s.t. \quad A^jy'&\leq 0 & j\in J\\ A^jy'&\leq 1 & j\notin J\\ y'_i&\geq -1 & i\notin I\\ y'_i&\geq 0 & i\in I \end{align*} \]
这里得说说拉格朗日函数,kkt,线性规划对偶的关系,考虑一个线性规划问题:
\[\begin{align*} \min \quad &c^Tx\\ s.t. \quad Ax&\geq b\\ x&\geq 0 \end{align*}\]
把他当成一个约束优化问题,写出拉格朗日函数:
\[ L(x,\lambda)=c^Tx-\lambda^T(Ax-b) \]
\(Ax-b\geq 0\),所以有\(c^Tx\geq L(x,\lambda)\),然后考虑拉格朗日函数的下确界:
\[ L(x,\lambda)=\lambda^Tb-(c^T-\lambda^TA)x \]
如果\(c^T-\lambda^TA> 0\),下界是\(-\inf\),如果\(c^T-\lambda^TA\leq 0\),下确界显然是\(\lambda^Tb\).
第二种情况就是线性规划的对偶问题了。\(c^Tx\geq L(x,\lambda) \geq \lambda^Tb\)
继续考虑restricted primal problem的对偶,首先由于restricted primal problem的最优解是大于0的, 上面那个对偶问题一定存在一个解\(y'>0\)(线性规划对偶都满足强对偶定理),利用原问题的对偶的可行解\(y\) 和上面的对偶问题的可行解\(y'\)构造一个新的对偶问题的可行解\(y'' =y+\epsilon y'\),并且显然\(b^Ty'' >b^Ty\),(\(\epsilon >0\))
这样可以得到一个更接近最优解的对偶问题可行解。
为了保证$y’’ $是一个对偶问题的可行解,要满足两个条件 1. \(y'' \geq 0\). 这需要\(\epsilon \leq \min_{y'_i<0}\frac{-y_i}{y'_i}\) 2. \(A^Ty'' \leq c\),这需要\(\epsilon \leq \min_{A^jy'>0}\frac{c_j-A^jy}{A^jy'}\)
得到$y’’ $之后重复上面的步骤,每次都能得到一个更接近最优解的对偶问题可行解.
2 an example
assignment problem (minimum-weight perfect matching problem in bipartite graphs)
integer program:
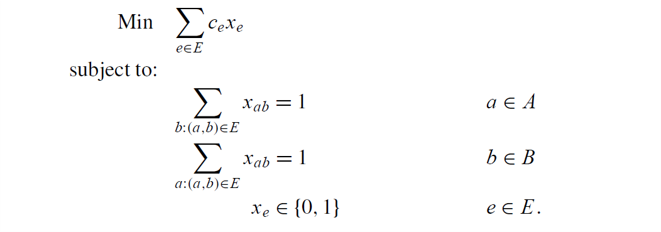
可以证明IP的线性松弛最优解是整数解。
dual of LP relaxation:
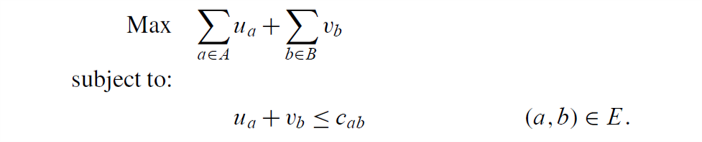
primal-dual 要从一个对偶问题的可行解开始。取\(u=v=0\)
restricted primal:
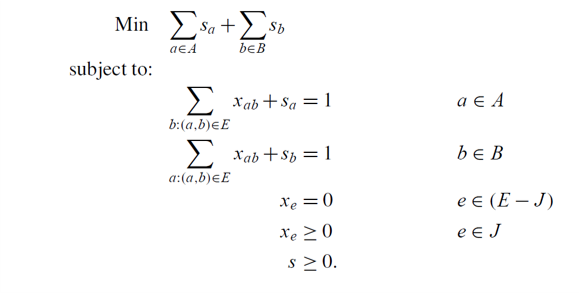
\(I=\emptyset,J=\{(a,b)\in E: u_a+v_b=c_{ab}\}\)
实际上可以证明restricted primal的基本可行解中的变量只能取0,1. 发现这是在求\(G=(A,B,J)\)上的最大匹配。
那么对于任意一个对偶问题的解,我们都能写出restricted primal问题,而restriced primal问题就是求一个二分图的最大匹配。 如果找到的最大匹配是一个完美匹配,可以发现restricted primal的目标函数值为0,说明找到了最优解,否则,继续写出restricted primal的对偶:
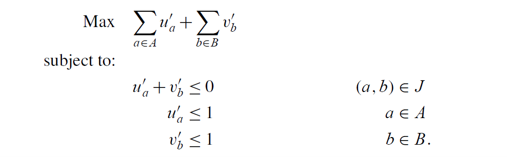
二分图上Maximum matching 的对偶实际上是 vertex cover, 在这里u取-1表示选择了这个点,取1表示没选这个点,max u恰好是在求最小顶点覆盖
上面对于assignment problem primal-dual方法给出了一个精确算法,但是过程中有两个条件难以满足: 1. 问题是由整数规划描述的,线性松弛的最优解恰好是整数解 2. 找到restricted primal problem之后直接发现了图上的对应问题,有已知的算法来解决这个问题
满足不了这两个条件,得到的就是一个近似算法。
整数规划一般不满足强对偶定理,因此对偶问题的最优解一般与原问题最优解不相等;restricted primal problem不一定容易解决,那么就放松互补松弛条件 >the central modification made to the primal-dual method is to enforce the primal complementary slackness conditions and relax the dual conditions
primal-dual方法是对偶问题的可行解出发,看是否有能同时满足互补松弛条件和原问题约束的原问题的解,现在由于条件2无法满足, restricted primal 及其对偶难解, 我们就只能根据 primal complementary slackness conditions ,从对偶解来计算原问题的解,而对于dual conditions,原问题约束有可能未被满足,有可能取等,有可能不取等,对于对偶问题变量是否取0未必有影响,因此只根据未被满足的原问题约束来想办法更新对偶解。
我觉得他的思路大概是这样的。
3 design rules
(不是记录design rules,是想搞清楚design rules是怎么来的)
原问题一般都能写成这样的整数规划:
\[ \begin{align*} \min \quad \sum_{e\in E}&c_ex_e\\ s.t. \quad \sum_{e\in \delta(S)}x_e&\geq f(S)\\ x_e&\in \{0,1\} \end{align*} \]
\(\delta(S)\)是把\(V\)分成\(S,V-S\)的一个割,\(f(S):2^{|V|}\rightarrow \mathbf{N}\)
书中是以hitting set problem 为例讲解的design rules,如果\(f(S):2^{|V|}\rightarrow \{0,1\}\),那么这就是hitting set problem了
hitting set problem:
Hitting set is an equivalent reformulation of Set Cover.(放到二分图上,分别是选左边和选右边)
NP-Complete.
Given subsets \(T_1,\ldots,T_p\) of a ground set \(E\) and given a nonnegative cost \(c_e\) for every element in \(E\), find a minimum-cost subset \(A\) s.t. \(A\cap T_i\not ={\emptyset}\) for \(i=1,\ldots,p\).
hitting set problem 既然是 NP-Complete 问题,很多常见问题都能建立hitting set的模型,上面的IP是把ground set当成图的所有割,需要hit的subsets当成 \(f(S)=1\)的那些割\(\delta(S)\)。
方便起见定义一些符号: * \(A=\{e:x_e=1\}\) * \(y\): dual variable * \(T_1,\ldots,T_p\) sets to be hit
根据part 2中的force primal complementary slackness conditions relax dual CSCs 的方法,
- \(y\rightarrow 0\)
- \(A\rightarrow \emptyset\)
- While \(\exists k\) : \(A\cap T_k=\emptyset\)
- \(\quad\)Increase \(y_k\) until \(\exists e\in T_k : \sum_{i:e\in T_i} y_i=c_e\)
- \(\quad\) \(A\rightarrow A\cup \{e\}\)
首先在3中,如何选择\(T_k\),如果存在多个\(T_k\)怎么选?
这要根据问题来确定。如果找到了多个\(T_k\)(称为一个violated set),我们可以同时增加对应的对偶变量\(y_k\),直到\(\exists e\notin A : \sum_{i:e\in T_i} y_i=c_e\).
由于整数规划的描述或者violation oracle可能没有严格返回\(f(S)=1\)的cut等问题(比如整数规划的约束是\(\leq\),对于正权无向图的s-t最短路来说最短路一定和每个s-t cut的交集正好都是一条边,然而换成\(\leq\)会让结果 变成单源最短路),\(A\)中的边可能会选的过多,去掉某些边也可能是可行解。由此可以在最后加入一个删边的过程,按照某种顺序(比如加入边的顺序)测试删掉某条边后\(A\)是否 仍是可行解,如果是就删掉这条边。

4 evaluate the performance guarantee
\[ \begin{align*} c(A)&=\sum_{e\in A} c_e\\ &=\sum_{e\in A}\sum_{i:e\in T_i}y_i\\ &=\sum_{i=1}^p|A\cap T_i|y_i \end{align*} \]
(2th -> 3th line: exchanging the two summations)
令\(\alpha=\max\{|A\cap T_i|\}\),根据\(\sum y_i\leq OPT\)容易得到
\[ c(A)\leq \alpha OPT \]
这种计算近似比的方法必须要得到A之后才能算出\(\alpha\),有些不便,引入一个 minimal augmentation set \(B\).(\(B\)是\(A\)加上极少数量的边从而成为一个可行解,从\(B\)中去掉任何一条边都不是可行解) 由于design rules中最后删边的过程,\(|A_f\cap T_i|\leq |B\cap T_i|\)(\(A_f\)是最终结果),那么对于任意当前解\(A\),我们找出对应的\(B\),分析最大的\(|B\cap T_i|\)(记为\(\beta\)), \(c(A)\leq \beta OPT\)。尽管minimal augmentation set听起来很复杂,这样可以在算法的执行过程中分析。
再考虑design rules中的violated set. 如果考虑每次取出的violated set \(\mathcal{V}_j\),有
\[y_i=\sum_{j:T_i\in \mathcal{V}_j}\epsilon_j\]
那么
\[ \begin{align*} \sum_{i=1}^p y_i&=\sum_{i=1}^p\sum_{j:T_i\in \mathcal{V}_j}\epsilon_j\\ &=\sum_{j=1}^{l} |\mathcal{V}_j|\epsilon_j \end{align*} \]
\[ \begin{align*} \sum_{i=1}^p|A_f\cap T_i|y_i&=\sum_{i=1}^p|A_f\cap T_i|\sum_{j:T_i\in \mathcal{V}_j}\epsilon_j\\ &=\sum_{j=1}^l(\sum_{T_i\in \mathcal{V}_j}|A_f\cap T_i|)\epsilon_j \end{align*} \]
比较\(\sum_{j=1}^l(\sum_{T_i\in \mathcal{V}_j}|A_f\cap T_i|)\epsilon_j\) 和 \(\sum_{j=1}^{l} |\mathcal{V}_j|\epsilon_j\),
if, for all \(j\in[l]\),
\[ \sum_{i=1}^p |A_f\cap T_i|\leq \gamma|\mathcal{V}_j| \]
then
\[ \begin{align} \sum_{i=1}^p|A_f\cap T_i|y_i&=\sum_{i=1}^p|A_f\cap T_i|\sum_{j:T_i\in \mathcal{V}_j}\epsilon_j\\ &=\sum_{j=1}^l(\sum_{T_i\in \mathcal{V}_j}|A_f\cap T_i|)\epsilon_j\\ &\leq \sum_{j=1}^l\gamma|\mathcal{V}_j|\epsilon_j\\ &=\gamma\sum_{i=1}^p y_i \end{align} \]
这还是需要先计算出\(A_f\),现在结合上minimal augmentation set \(B\),
\[ \sum_{i=1}^p |A_f\cap T_i|\leq \sum_{T_i\in \mathcal{V}(A)}|B\cap T_i| \leq \gamma|\mathcal{V}_j| \]
同上,\(\gamma\)就是近似比。
再进一步考虑如果violation oracle返回的\(\mathcal{V}\)中有\(f(S)=0\)的cut,那么与上文类似,
\[ \sum_{T_i\in \mathcal{V}(A)}|B\cap T_i| \leq \gamma c \]
\(c\)是\(\mathcal{V}(A)\)中\(f(S)=1\)的cut的数量。
design rules 并不是一定最优,只是对于某些问题这样做挺好,对于这些design rules 现在都有办法通过分析设计出的近似算法的过程来确定近似比了。
5 notes
后来在读 the design of approximation algorithms 中的 chap 7.
首先Theorem 7.1的定理\(f=\max{|\{j:e_i\in S_j\}|}\)是近似比,就是part3 中的 evaluate the performance guarantee 部分第一个定理(参数是\(\alpha\)那个)
对于part2中说到的近似算法放松互补松弛条件(CSC),这里又更详细的解释: - enforce primal CSC 意味着如果\(x_i>0\),\(x_i\)在对偶问题里对应的不等式取等。 - relax dual CSC 如果某个对偶变量\(y_i>0\),在原问题里对应的约束不等式却未必取等。
求近似比的部分中\(f=\max{|\{j:e_i\in S_j\}|}=\sum_{j:e_i\in S_j}x_j\) 也就是\(y_i>0\)在原问题中对应的约束不等式左侧。
因此 relax dual CSC 保证了近似比,而 enforce primal CSC 提供了通过对偶构造原问题可行解的方法。
整数规划的对偶应该是什么样的?对于同一个问题,不同的整数规划建模的对偶最优解都相同吗?
整数规划没有严格意义上的对偶,但是有个叫拉格朗日对偶的东西。
对于同一个问题不同整数规划建模对偶的最优解是不一样的,不同建模的线性松弛最优解都不一样。
拉格朗日对偶大概是这样的东西:(看了知乎上某人的integer programming翻译,我推了一下,但基本上变成latex公式输入练习了。。。) part1中有一点拉格朗日函数和对偶的部分,那里用的原问题是一个线性规划, 把他变成整数规划,加入一个\(x\in X\subset Z\)的约束,然后求\(\max_{\lambda}\min_{x}\lambda^Tb-(c^T-\lambda^TA)x\) (在\(x\in X\subset Z\)的约束下)实际上也就是通过调整\(\lambda\),让拉格朗日函数的下确界尽量大。
我总觉得这里拉格朗日函数的最小值就是原来的整数规划最优解,但是实际上不是,拉格朗日函数已经是原问题的松弛了,因为在拉格朗日函数中,扔掉了\(Ax-b\geq 0\)这个 约束,后面的过程根本没有考虑过\(Ax-b\geq 0\)这个约束
IP:
\[ \begin{align*} \min \quad &c^Tx\\ s.t. \quad Ax&\geq b\\ x&\geq 0\\ x&\in Z \end{align*} \]
构造\(f(x)=c^Tx-\mu^T(Ax-b)\leq c^Tx\)(let \(\mu\leq 0\))
\(f(x)\)的下确界尽量大:\(g(\mu)=\max_{\mu}\min_{x}(c^T-\mu^TA)x+\mu^Tb\)
写成线性规划的形式:
\[ \begin{align*} \min \quad &\eta\\ s.t. \quad (c^T-\mu^TA)x_1+\mu^Tb&\geq \eta\\ (c^T-\mu^TA)x_2+\mu^Tb&\geq \eta\\ &\ldots\\ (c^T-\mu^TA)x_n+\mu^Tb&\geq \eta\\ \mu &\geq 0\\ \eta &\in R \end{align*} \]
然后写出上面的线性规划的对偶:
\[ \begin{align*} \min \quad \sum_{i=1}^n \lambda_i(c^Tx_i)&\\ s.t. \quad \sum_{i=1}^n \lambda_i (Ax_i-b)&\geq 0\\ \sum_{i=1}^n \lambda_i &= 1\\ \lambda &\geq 0 \end{align*} \]
把此处的\(x_i\in Z\)放大为\(x_i\in R\), 由于\(x_i\in R, x_i\geq 0\)是凸集,所以\(x=\sum_{i=1}^n \lambda_i x_i\in R\),上面的对偶可以直接改写为整数规划的线性松弛。
这说明了通过调整乘子来让拉格朗日函数的下确界最大的这种这种方法获得的解要比线性松弛的解更好,因为上面有一个把\(x\in Z\)放大到\(x\in R\)的过程。
然后我就发现了一个问题,观察\(g(\mu)=\max_{\mu}\min_{x}(c^T-\mu^TA)x+\mu^Tb\),发现如果取某个\(\mu\)使得\(c^T-\mu^TA\)的某一项是小于0的, 由于\(x\)在这里的范围是\(0\leq x \in Z\),为了取到\(\min\),\(x\)对应分量就会取正无穷,那么下确界也就是负无穷了,无法得到一个有效的对偶,因此 取\(\mu\)必须满足\((c^T-\mu^TA)\geq 0\),这样一来\(x\)一定会取到\(\mathbf{0}\),下确界也就是\(\mu^Tb\),写成一个线性规划问题竟然和原来的整数规划的 线性松弛的对偶一样,但是根据刚刚的证明拉格朗日函数下确界的这种方法应该比线性松弛获得的解更好。
我觉得问题在于:上一段的简单分析应该是没有错误的,这也是为什么 integer programming 中讲拉格朗日对偶只是把一部分约束放入函数中。在处理的过程中, \(Ax-b\)被扔到了目标函数里面去,而\(x\)的取值范围并没有保证\(Ax-b\geq 0\)。实际上如果把所有约束都放到目标函数内的话拉格朗日对偶就是和线性松弛的对偶一样的。 观察上面\(x_i\in Z\)放大为\(x_i\in R\)的部分,实际上\(x_i\)是各个分量大于等于0的所有n维整数向量,他们构成的凸包和\(x_i\in R\)构成的完全一样。
6 random thoughts
从寒假开始也算是看了两本书关于 primal-dual 方法的章节。
大多数问题的建模都是整数规划,primal-dual 用的是线性松弛的对偶,找到的可行解也不会比线性松弛的最优解更好, 只有线性松弛的解和整数规划相比比较接近才有很好的近似比,如果像是 feedback vertex set 用hitting set建模的整数规划,这种线性松弛最优解近似比是logn级别, primal-dual近似比最好也只能做到logn级别了,但是最短路的hitting set建模线性松弛最优解和整数规划最优解相等,primal-dual甚至能得出精确算法(dijkstra), 同样的问题,不同的整数规划建模方法,就有不同的线性松弛,就有不同的近似比。
为什么不直接解线性松弛而要用primal-dual?我觉得主要原因是原来的整数规划约束个数可能是指数级别,解线性规划会解不出, 但是primal-dual有时候(Violation Oracle能很快给出还没满足的约束)需要维护的对偶变量数量只是多项式级别的。
要用primal-dual方法解决一个问题,需要考虑 - 用什么方法来写出整数规划,是否能找出一个能用的Violation Oracle,线性松弛是否有一个好的近似比 - 根据具体问题是否有好用的design rules,按照什么方法和顺序找violated set等,复杂度又如何 - 怎么分析近似比,能不能做到线性松弛的近似比一样的级别
我发现大概这个整数规划约束有指数多个,一般整数规划和线性松弛差的不大。
对比The primal-dual method for approximation algorithms and its application to network design problems, chapter 4这个章节和The Design of Approximation Algorithms chapter 7, 明显后者更加简单易懂,使用了很多例子,但是我觉得前者要系统很多,而且更加符合逻辑和直觉。首先介绍什么是classic primal-dual method,从这个方法出发有了设计近似算法的基本框架,如何从整数规划的线性松弛和LP的对偶 找到原问题(IP)的可行解,以及后面对用hitting set建模抽象出来的函数\(f(S)\)的讨论,而后者通过众多例子介绍了primal-dual,比较易懂,但是关键部分的近似比证明受例子的影响,没有一般化,感觉很难想到。
根据之前看的两本书,做了slides.